„A természet nagy könyve a matematika nyelvén íródott” – mondta Galileo Galilei, s ki vagyok én, hogy a híres természettudós állítását megkérdőjelezzem?
Írta: Székely Ágnes (Magyar Természettudományi Múzeum Mátra Múzeuma)

Múzeumpedagógusként rengeteg foglalkozást tartottam már a gyöngyösi Mátra Múzeum kiállítótereiben. Számos tárlatot vezettem a Természettudományi Pavilon háromszintes kiállításában és a Pálmaházban, ahol nemcsak egzotikus növényekkel találkozhatnak a látogatók, de élő állatokat (halakat, kétéltűeket, hüllőket, madarakat és ízeltlábúakat) is megfigyelhetnek. Most először megpróbálom a matematikus szemével végigjárni a természetrajzi kiállítást.

A kiállítás elrendezése
Mivel az emberek mindig is harmóniára törekedtek környezetük kialakításakor, ez az igény a kiállítások rendezésénél is megmutatkozik. A három szinten összesen 24 dioráma található kör alakú vitrinekben, melyek egymással párhuzamosan sorakoznak, szimmetrikusan elrendezve, négy-négy egymással szemben. A kiállítás központi eleme, a monumentális kocsánytalan tölgy akár egy óriási tükör áll középen.


A középső szint központi terét a körbejárható, úgynevezett koporsóvitrinek foglalják el, ezek egymástól egyenlő távolságra helyezkednek el. Az élővilág két legnépesebb csoportját, a puhatestűeket és az ízeltlábúakat mutatják be.

A legfelső szinten a madarak királyaként egy parlagi saspár uralja a fát. Az egyik kör alapterületű vitrinben a hazai emlősök egy része kapott helyet, a másikban távoli tájak madaraira csodálkozhatunk rá.
Most pedig nézzünk pár példát a különböző matematikai fogalmakra, melyekkel a természetben találkozhatunk.
Szimmetriaviszonyok
Az élővilágban mindenféle szimmetriaviszonyra találunk példát.
Aszimmetria = nincs szimmetria; a szivacsokra jellemző – a kiállításban csak képen szerepelnek.
Gömbszimmetria = végtelen – vagy sok, de véges – számú szimmetriatengellyel leírható megjelenési formák, például egyes gömbölyű termések, petecsomók, gubacsok.
Sugaras szimmetria = egy szimmetriatengellyel és számos szimmetriasíkkal bíró élőlények; ilyenek a kalapos gombák alulnézetben. A növényvilágban nagyon sok virágalkotó elrendeződésében tapasztalhatunk sugaras szimmetriát. Egyes madarak fészke (megközelítőleg) kör alakú.

Napraforgó virága a „Konyhakert” című diorámában – Feketerigó fészke a tojáskiállításban
A sugaras szimmetriájú állatok – például a csalánozók – minden irányban nagyjából egyenlő eséllyel reagálnak a környezeti hatásokra: így képesek statikus helyzetüket megtartani a vízáramlással szemben, vagy éppen hatékonyan zsákmányt gyűjteni.
Bilaterális (kétoldali) szimmetria = egyetlen szimmetriasíkkal bír, az élővilág nagy részére ez a jellemző. A növényeknél a legszembetűnőbb példája a kétoldali részarányosságnak a levelek felépítése.

Levélfa (Monstera deliciosa) levele (Pálmaház) – Kapotnyak (Arum maculatum) levele (a kiállítási tölgyfa tövében)
Az élet a vízben keletkezett, az első mozgásformák is itt alakultak ki. Ha egy test pontosan és egyenes vonalban próbál mozogni, szimmetrikusnak kell lennie. Ha a test aszimmetrikus, a rá ható ellenállási erők nem egyenlítik ki egymást, így a test nem tarthatja meg egyenes pályáját. Az irányított mozgás során a bilaterális szimmetria bizonyult a legelőnyösebbnek és leghatékonyabbnak.

Szívkagyló (Cardium costatum) – Ázsiai orrszarvúbogár (Eupatorus gracilicornis)

Kanalasgém – Őzsuta – Vaddisznó hátulsó lába
Párhuzamos vonalak
Szinte mindenhol felfedezhetjük a párhuzamosság példáit a növény- és állatvilágban (és a kiállítás-rendezésben). A mértanban a párhuzamosság két mértani alakzat viszonyát jelenti. Két egyenes akkor párhuzamos, ha egy síkban vannak, és nem metszik egymást.

Évgyűrűk (a felülnézet körkörös) – Nád – Bogarak a rovardobozokban
Mértani alakzatok
Igen gyakori alakzat a természetben a gömb, amelyet a matematikusok gyakran neveznek a „legtökéletesebb mértani alakzatnak".

Pálma gömbölyű termései a Pálmaházban
A méhek viszont a hatszöget választották sejtjeik építéséhez, mert így optimális az anyag és a tér kihasználása. A legkevesebb méhviasz felhasználásával a legtöbb méz tárolására alkalmas helyszínt alkotják így meg, ez ugyanis az a forma, amelyből hézagmentesen lehet építkezni, és a legtöbb méz fér bele.

Élő méhek a kaptárjukban – Kígyóbőr
A hüllők pikkelyei (melyek gyakran rombusz illetve téglalap alakúak) a fajok azonosítására alkalmas bélyegek.
Aranymetszés
Az aranymetszés két rész egymáshoz való viszonya, mely a következőképpen írható le: két rész az aranymetszés szerint akkor aránylik egymáshoz, ha az egész (a + b) úgy aránylik a nagyobbik részhez (a), ahogy a nagyobbik rész a kisebbikhez (b):
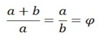 Ezt a különleges viszonyt gyakran nevezték a történelem folyamán „univerzális törvénynek”. A kiállításban pedig például lepkeszárnyak szemléltetik.
Ezt a különleges viszonyt gyakran nevezték a történelem folyamán „univerzális törvénynek”. A kiállításban pedig például lepkeszárnyak szemléltetik.

Hebomoia glaucippe – Saturnia pyri
Fibonacci-sorozat
A számsor lényege, hogy minden szám az előző két szám összege:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 …
Leonardo Fibonacci (1170–1250) itáliai matematikus a szaporodó nyulak számán elmélkedve alkotta meg a számsort 1202-ben. Egyébként neki köszönhetjük az arab számok elterjesztését is Európában a Liber Abaci című könyvével.
Számos növénynél felfedezhetjük a Fibonacci-számok egyikét – például a vitorlavirágnak (a múzeum Pálmaházában) 1 (ami nem is szirom), a hóvirágnak 3, a vadalmának 5 szirma van. A napraforgó tányérján 55 vagy 89 mag van, ráadásul Fibonacci-spirálban rendeződve. Ugyanis ha a Fibonacci-számokat négyszögek oldalának hosszaként használjuk fel, a négyszögeket egymás mellé rakjuk, és pontjaikat körívekkel összekötjük, akkor spirális alakzatot kapunk. Ebbe a spirálba rendeződnek a fenyőtoboz pikkelyei, illetve a csigáspolip (Nautilus pompilius) házát felépítő légkamrák (mind a recens, mind a kihalt fajoknál, ez utóbbit a márványpadlóban fedezhetik fel a szemfüles látogatók).

Vitorlavirág – Fenyőtoboz – Ma élő csigáspolip és kihalt rokona
A Fibonacci-spirált gyakran hasonlítják az ún. aranyspirálhoz, amely nem más, mint az aranymetszésből ismert Fi alapú logaritmikus spirál. Ezt sok élőlény próbálja követni, azon egyszerű oknál fogva, hogy ez a legjobb módszer az arányos növekedésre, illetve a leghatékonyabb térkitöltésre. A Fi irracionális szám, közelítő értéke 1,618. A Fibonacci-számsor elemeire 55-től kezdődően valóban igaz, hogy az egymást követő számok hányadosai egyre jobban közelítik ezt az értéket, ebből adódóan a Fibonacci-spirál és az aranyspirál között csak közelebbről szemügyre véve vehető észre a különbség.
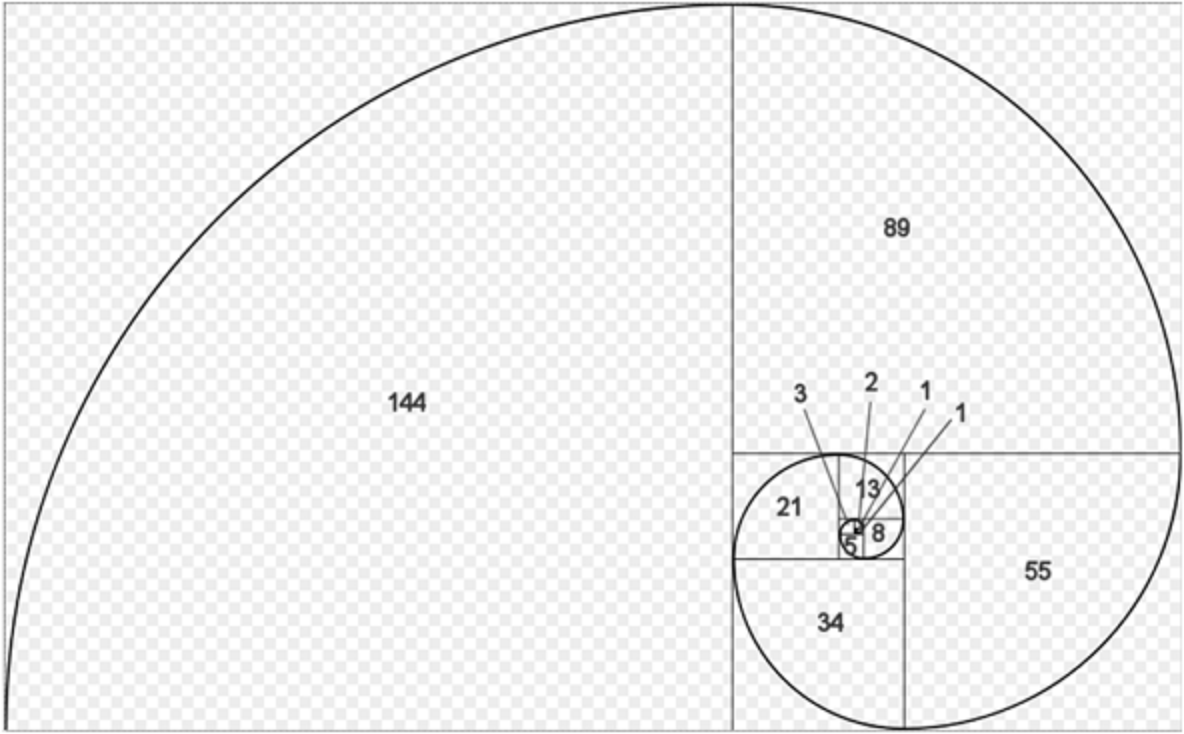
Fibonacci-spirál (forrás: Thinglink)
Fraktálok
A fraktálok olyan mértani alakzatok, amelyek kisebb részekre bonthatók, és ezek a kisebb részek – ha csak megközelítőleg is, de – a teljes alakzat másolatai kicsiben. A természetben is megtalálható fraktálok például a karfiol rózsája, a fák ágainak elrendeződése.

Kövirózsák az egyik terráriumban
A gekkók lábujjainak végén amolyan mikroszkopikus fastruktúraként több szinten át elágazó, a végső lépcsőben már nanométeres tartományig vékonyuló bolyhok (ágacskák) vannak, és ezek illeszkednek bele azokba a mikroszkopikus hasadékokba, amelyek minden felületre jellemzőek.

Gekkóláb, az ujjak végén tapadószőrökkel, és azok elektronmikroszkópos képe (forrás: Fizikai Szemle) – Madagaszkári nappaligekkó (Phelsuma madagascariensis) (forrás: Pinterest)
Csíkok, pöttyök és minták
Kevésbé ismert, de a szép és változatos természetes mintázatok leírhatóak matematikai egyenletekkel.

Hím ezüstfácán – Foltos szalamandra – Tigrisszalamandra (észak-amerikai faj), élő egyed

Sebes pisztráng a „Hegyi patak” című diorámában
Ha nincs forrás feltüntetve, a képeket Székely Ágnes illetve a Mátra Múzeum készítette.
Felhasznált irodalom
http://www.erdekesvilag.hu/egy-nagyszeru-video-a-szamok-es-a-termeszet-osszefuggeseirol/
https://www.mozaweb.hu/Lecke-BIO-Biologia_10-Az_allatok_szervezodesi_szintjei-104957
http://fizikaiszemle.hu/archivum/fsz0506/vicsek0506.html
http://www.termeszetvilaga.hu/tv2002/tv0207/szimmetria.html
http://www.matud.iif.hu/2017/02/02.htm
http://hvg.hu/instant_tudomany/20140724_miert_hatszogekkel_dolgoznak_a_mehek
http://curiocity.blog.hu/2014/10/12/miert_pont_a_fibonacci_szamok_mozgatjak_a_vilagmindenseget
A bejegyzés trackback címe:
Kommentek:
A hozzászólások a vonatkozó jogszabályok értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a Felhasználási feltételekben és az adatvédelmi tájékoztatóban.
kéki béla 2020.04.09. 05:47:30
múzeum · https://www.nhmus.hu/ 2020.04.09. 13:34:36
Örülök, ha tetszett, öröm az ilyen posztok születésében részt venni. De vannak, akik inkább életmód-tanácsadásos cikkeket szeretnek, és ezzel nincs baj. (Néha én is olvasok ilyesmit.)
Egy adott korban vagy pillanatban az emberiség produktumainak nagy része "hulladék". Így volt ez a barokk zene vagy a 20. századi autógyártás esetében is, és ez a helyzet ma is. Ez így van jól, ugyanis a sokaság felett ítéletet mond az idő; a gyenge és a középszerű feledésbe merül, és ami érték, megmarad. Bach, Händel és Schütz zenéje ma is itt van, ahogy a Land Rover és a Ferrari is. De ezek a "hulladékból" emelkedtek ki; a gyenge teljesítmények tanulsága kellett a jók megszületéséhez.
Merkl Ottó





